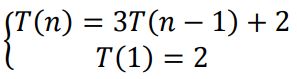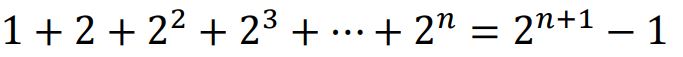Solve for the following recurrence equation in terms of 𝑛:

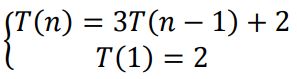
T(n) = 3T(n-1) + 2
     = 3[3T(n-2) + 2] + 2 
     = 32T(n-2) + 3 * 2 + 2
     = 32[3T(n-3) + 2] + 3 * 2 + 2
     = 33T(n-3) + 32 * 2 + 3 * 2 + 2
     = 33[3T(n-4) + 2] + 32 * 2 + 3 * 2 + 2
     = 34T(n-4) + 33 * 2 + 32 * 2 + 3 * 2 + 2  
     = 34[3T(n-5) + 2] + 33 * 2 + 32 * 2 + 3 * 2 + 2
     = 35T(n-5) + 34 * 2 + 33 * 2 + 32 * 2 + 3 * 2 + 2 
     = ...
     = 3kT(n-k) + 3k-1 * 2 + ... + 33 * 2 + 32 * 2 + 3 * 2 + 2 
       (Let n-k = 1, we will have k = n-1)
     = 3n-1T(1) + 3n-1-1 * 2 + ... + 33 * 2 + 32 * 2 + 3 * 2 + 2 
     = 3n-1*2 + 3n-2 * 2 + ... + 33 * 2 + 32 * 2 + 3 * 2 + 2
     = 2 * (3n-1 + 3n-2 + ... + 33 + 32 + 3  + 1)

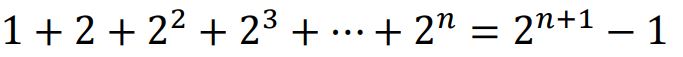
     = 2 * (3n - 1)
     = 2 * 3n - 2