Parse Trees - hierarchical structure

Ambiguity:   A grammar has more than one parse tree.

The grammar is the following:

<assign> → <id> = <expr>
<id> → A | B | C
<expr> → <expr> + <expr>
         | <expr> * <expr>
         | ( <expr> )
         | <id>
The sentence
           A = B + C * A
                                                        has two distinct parse trees.
(See figure 3.2 right parse tree and left parse tree on page 119)

 
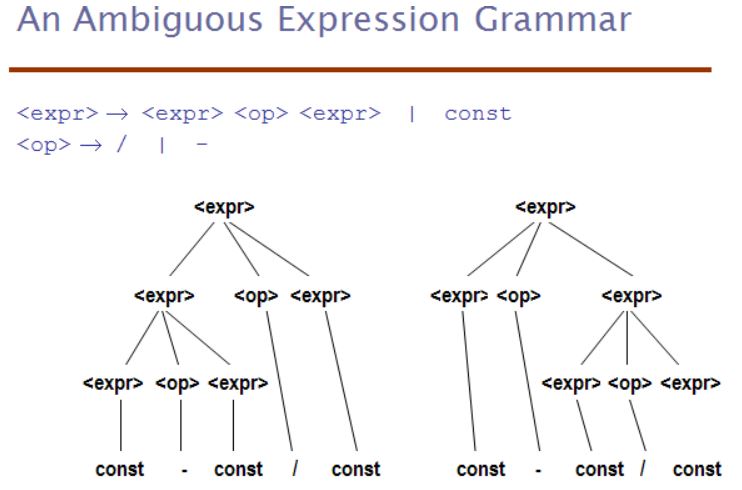
In the above left parse tree, the multiplication operator is generated lower in the tree, which could indicate that it has precedence over the addition operator in the expression.  However, the above right parse indicates just the opposite.  So, these two conflict on precedence of operators. 

There is an unambiguous grammar for the above expression which follow the order of MATH.
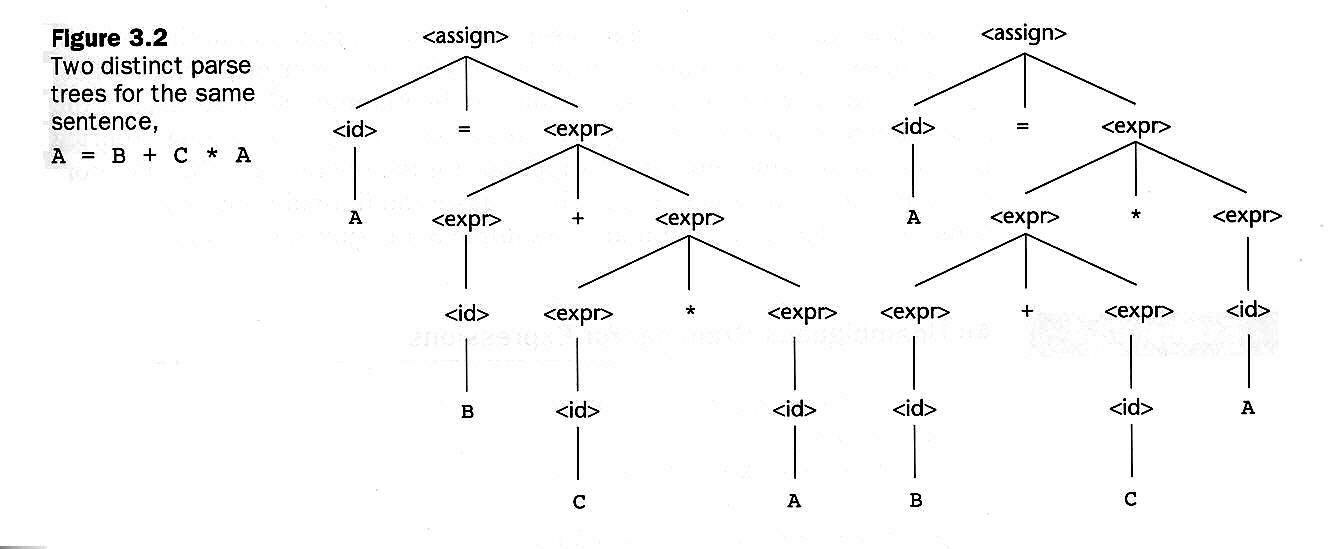
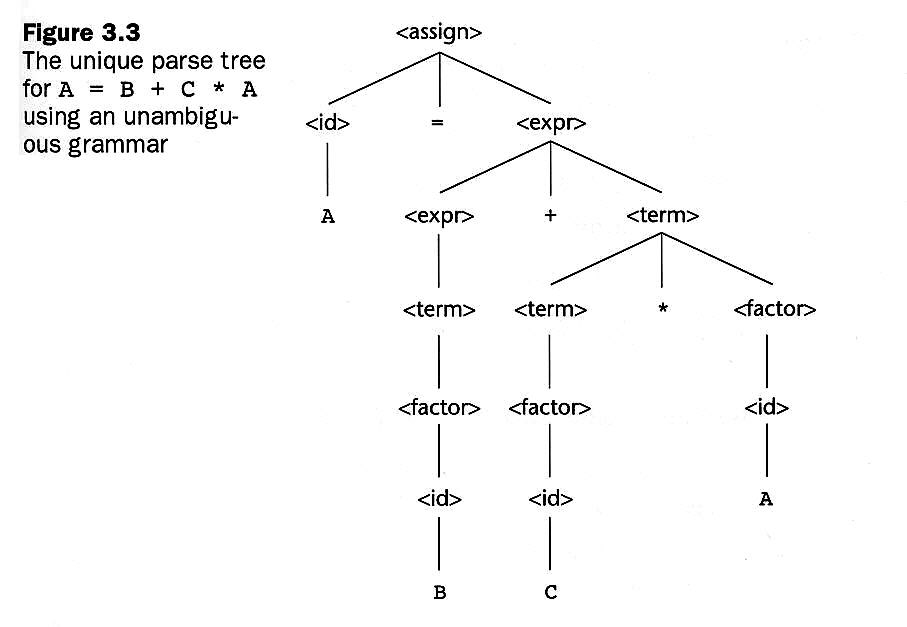
(See Example 3.4 on page 120)  There is an additional nonterminal, <term>.

<assign> → <id> = <expr>
<id> → A | B | C
<expr> → <expr> + <term>
         |  <term>
<term> → <term> * <factor>
         |  <factor>
<factor> → ( <expr> )
          | <id>
No matter, you get from leftmost derivation or rightmost derivation,
there is only one parse tree for the sentence A = B + C * A.
 
Leftmost derivation:
<assign> => <id> = <expr>
         => A = <expr>
         => A = <expr> + <term>
         => A = <term> + <term>
         => A = <factor> + <term>
         => A = <id> + <term>
         => A = B + <term>
         => A = B + <term> * <factor>
         => A = B + <factor> * <factor>
         => A = B + <id> * <factor>
         => A = B + C * <factor>
         => A = B + C * <id>
         => A = B + C * A		 Rightmost derivation:
<assign> => <id> = <expr>
                    => <id> = <expr> + <term>
                    => <id> = <expr> + <term> * <factor>
                    => <id> = <expr> + <term> * <id>
                    => <id> = <expr> + <term> * A
                    => <id> = <expr> + <factor> * A
                    => <id> = <expr> + <id> * A
                    => <id> = <expr> + C * A
                    => <id> = <term> + C * A
                    => <id> = <factor> + C * A
                    => <id> = <id> + C * A
                    => <id> = B + C * A
                    => A = B + C * A

Exercise: Show a parse tree and leftmost derivation for A = C * B + A


For the statement, A = B + C + A, you may have the following sequences of computation:
1. do B + C first, after that sum of B and C adds A, i.e. A = (B + C) + A
2. do C + A first, after that B adds sum of C and A, i.e. A = B + (C + A)
In mathematics, methods 1 & 2 get the same result.
In computer science,
    1. If it is "integer computer arithmetic", both methods get the same result.
    2. If it is "floating-point addition", two methods produce different results.
        e.g..  Let floating-point values store seven digits of accuracy.
              If we have a number 12,345,670 which will be stored as 1.234567*107.
              (1.234567*107 + 1) + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
      =1.234567*107 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
      =(1.234567*107 + 1) + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
      =1.234567*107 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
      =(1.234567*107 + 1) + 1 + 1 + 1 + 1 + 1 + 1 + 1
      =1.234567*107 + 1 + 1 + 1 + 1 + 1 + 1 + 1
      Keep going....  The answer =1.234567*107
      1.234567*107 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
      =1.234567*107 + (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1)
      =1.234567*107 + 10 The answer =1.234568*107
    1.234567*107 is not equal to 1.234568*107

Look at page 130:

For the following grammar:
<if_stmt> → if <logic_expr> then <stmt>
            |  if <logic_expr> then <stmt> else <stmt>
<stmt> → <if_stmt> | <any non-if statement>
We can prove it as an Ambiguous Grammar:
<if_stmt> → if <logic_expr> then if <logic_expr> then <stmt> else <stmt>
Note:     Which "if" does "else" match to?  Most recent one?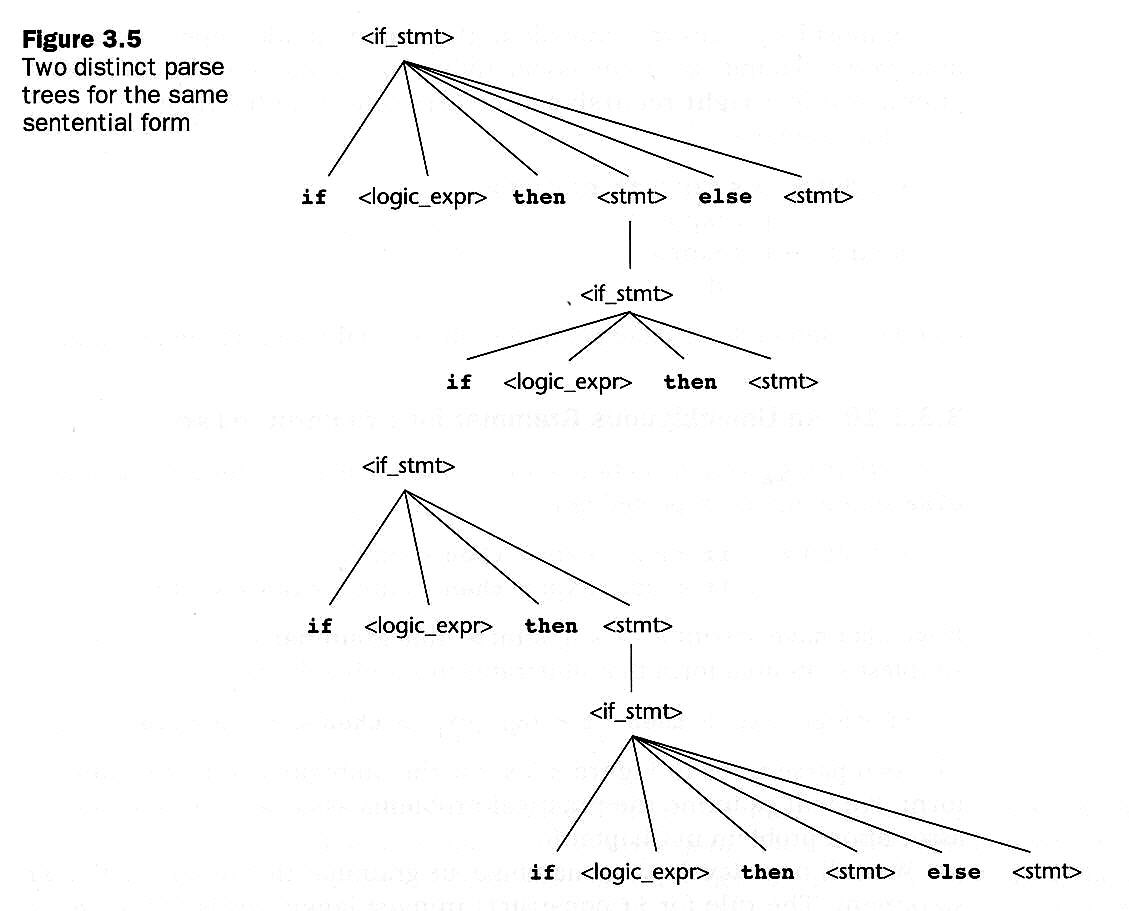

Unambiguous Grammar:  (Page 132)

Exercise: Write a derivation & draw a parse tree for the following statement by the above grammar:
<stmt> → if <logic_expr> then if <logic_expr> then <stmt> else <stmt>
BNF (Backus-Naur Form): collection of rules, method of syntax description.  (See page 110)
BNF rule:  replace from the beginning of right side (= left associatively)
BNF rule:  replace from the end of right side (= right associatively)
e.g.. exponentiation should be right associative.

Example: (page 126)